はじめてのA/Bテスト、前篇に続き後編となります。（前篇は「はじめてのA/Bテト（前篇）」）

今回はA/Bテストの仮説検定ステップについてまとめたいと思います。前篇同様、主な参考文献は『A/Bテスト実践ガイド 真のデータドリブンへ至る信用できる実践とは』（アスキードワンゴ）です。

 

統計学的検定をする意味

前半篇で実験デザインをして、データが収集できたと仮定します。

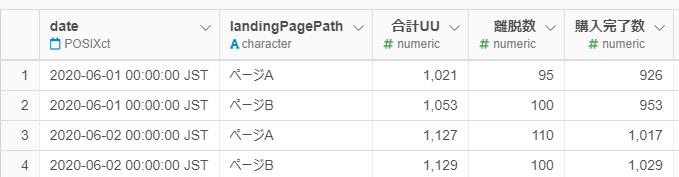
データセットは①日付②ページ名③合計UU数（購入開始をしたユニークユーザー）④合計UU数から購入完了数を引いた離脱数⑤購入完了数の5つの列です。ページAが介入群（クーポンコードを表示するUIに変更したページを見せるグループ)、ページBがコントロール群（既存のUIを見せるグループ）とします。

▼データイメージ

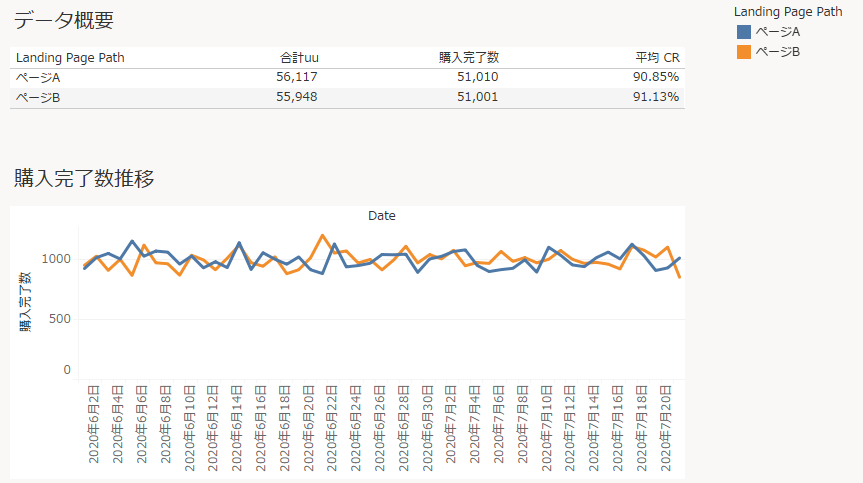
▼以下データ概要を単純に可視化してみました。

可視化データを見て、ページAとB結局どちらがいいのかなかなか難しいですね。平均CRはページBの方が高いですが、もしかしたらこの差には意味がなく”たまたま”かもしれません。そんな時に「確率的に偶然や誤差とは考えにくく、意味があると考えられる」というために必要なステップが「統計学的検定」となります。

検定の種類

2グループの違いを検定する方法として、よく用いられる方法の一つは「t検定」や「カイ二乗検定」と呼ばれる頻度論的方法、もう一つは「ベイジアンA/Bテスト」と呼ばれるベイズ統計の方法があります。

頻度論的アプローチはオーソドックスな方法ですが、ビジネス的な要求からベイジアンA/Bテストを採用するケースもあるようです。ここではカイ二乗検定とベイジアンA/Bテストについて、Exploratoryで操作しながらみていきます。

ちなみに、頻度論的差の検定はいくつか方法があります。今回は購入完了率の差（「割合の差」）を比較したい、かつデータが正規分布に従うためカイ二乗検定を利用します。目的変数が連続変数の場合（「平均の差」の検定）、t検定を利用できます。（検定の使い分けは、「A/Bテストに用いられれる統計的検定手法（ロジック）のまとめ＆比較」が参考にります）

 

カイ二乗検定（頻度論的アプローチ）と結果の解釈

仮説	購入確認ページにクーポンコード入力欄を追加すると、購入プロセスを開始したユーザー1人当たりの購入完了率が低下する
反証したい仮説	購入確認ページにクーポンコードを表示しても、1人当たりの購入完了率は低下しない
基準値	p値<0.05（ABグループ間で生じた差がたまたまである割合は5%以下）

 

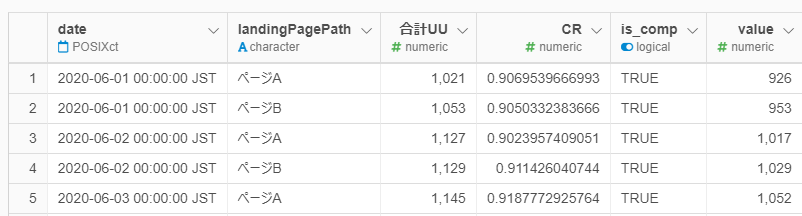
Exploratoryでのカイ二乗検定の操作自体は大変簡単ですが、カイ二乗検定の特性上データの持ち方を以下のように変更する必要があります。購入完了の有無を論理型で1列、その時の値を更に1列持つ必要があります。この加工方法に関してはExploratoryさんの記事をご参考にしてください。

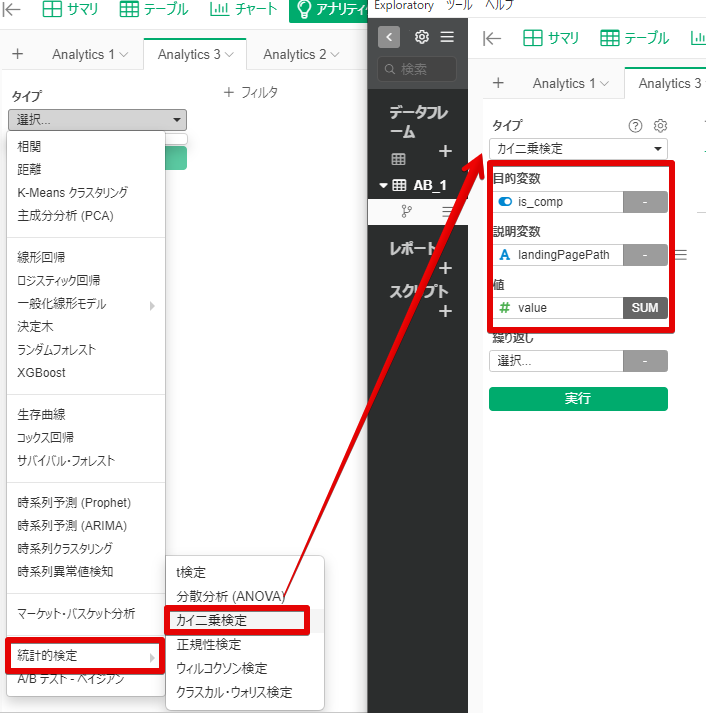
さて、具体的な操作は以下です。

アナリティクス＞タイプ＞統計的検定＞カイ二乗検定を選択。目的変数に確認したい変数（購入完了完了しているか否か）を選択、説明変数にlandingPagePathを入れ、値にvalueをいれます。これで検定結果が出ます。

検定結果は、以下になります。P値が0.13です。偶然ABグループに差が生じる割合が13%あり、目標としていた5%とはかけ離れてしまいました。つまり「購入確認ページにクーポンコード入力欄を追加すると、購入プロセスを開始したユーザー1人当たりの購入完了率が低下する」とは言えませんでした。しかしこの結果を経営陣に「結果は有意ではありませんでした。」と報告しても「So What!?」が返ってくる恐れがあります‥‥（※サンプルデータのため、検出力が目標としていた80%に届いていない点ご容赦ください）

上記のような例を含め、頻度論的アプローチのデメリットとしてよく指摘される点は以下4点が多い気がします。

1	テスト開始前に、サンプルサイズの検討などある程度統計的知識が必要な作業を要す
2	サンプルが集まってからでないと検定ができないので、タイムラグが生じる
3	検定結果は直観的に理解しづらい（P値とは…から説明しなければいけない）
4	有意か有意ではないかの白黒の判断しかできないので、ビジネス的にネクストステップが決めづらい

 

そこで、ベイジアンA/Bテストというベイズ推定を用いた推定を…という流れなのですが、『A/Bテスト実践ガイド』の著者Ron Kohavi氏は、頻度論的アプローチによる検定結果をビジネス的に解釈する方法も紹介しています。

確かにベイジアンA/Bテストというと敷居が高い気がしてしまいますが、t検定やカイ二乗検定はExcelでもできますので、そちらの方が有難いというケースもあると思います。

Ronさんが強調するのは、施策の実用性と統計学的有意性の掛け算で検定結果を解釈するという点です。書籍ないで紹介していた解釈をご紹介します。今回は2番の解釈、、、でしょうか（クーポン発行は手続きやコードの管理、改修運用コストがかかる、統計的有意でないという結果）

検定結果	実用性	解釈
有意でない	実用性は低	施策にあまり意味はない
有意	実用性あり	ローンチの決定に動きだせる
有意	実用性低	ローンチをに対するコストパフォーマンスを検討する必要がある
有意でない	実用性ありそう	テストを再度実施すべきで、結果の精度を上げるためにより大きな検出力テストを再度実施すべき

『A/Bテスト実践ガイド』Kindle 位置No.1245-1247）より要約

 

ベイジアンA/Bテスト

では、ベイジアンA/BテストをExploratoryでやってみます。

ベイジアンA/Bテストでは、ベイズ推定を使用してAとBどちらがより優れているか、その確率を示します。ベイジアンA/Bテストのメリットは頻度論的アプローチのデメリットの逆と考えて頂ければOKです。特にサンプルサイズが小さい早い段階でも検証できるというのがメリットといわれます。

また頻度論的アプローチとの大きな違いとして、「事前確率」「事後確率」を仮定できます。

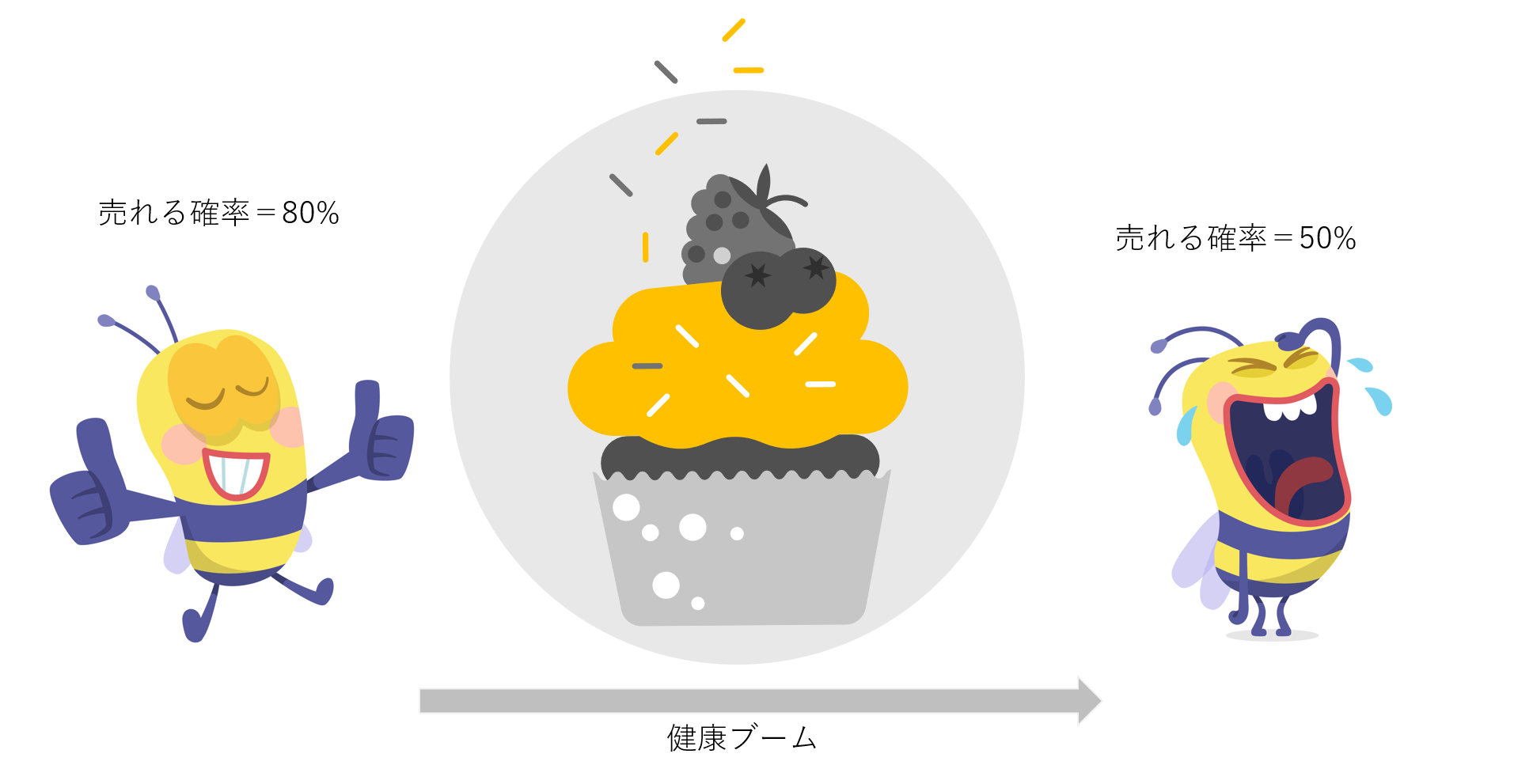
例えば、新作ケーキの発売で考えてみましょう。開発途中は過去の実績なども考慮し、売れる確率は70%、売れない確率は30%と仮定していたとします。これが「事前確率」です。しかし発売してみると突如健康ブームが到来し、思うほど売れ行きがあがりません。この時、追加された販売実績データによって売れる確率は50%と修正されます。これをベイズ更新と呼びますが、経験などに基づく人の学習方法とよく似た操作をベイズ推定では数学的に実現します。

 

ExploratoryでベイジアンA/Bテストを実施してみます。

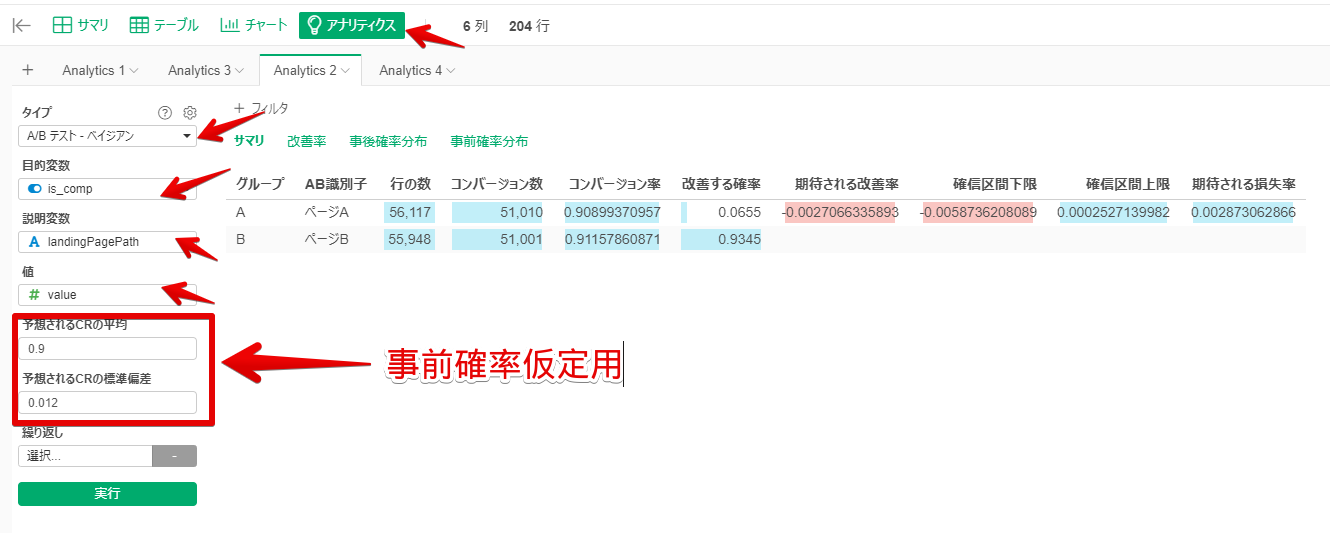
アナリティクス＞A/Bテスト‐ベイジアン＞目的変数に確認したい変数（購入完了完了しているか否か）を選択、説明変数にlandingPagePathを入れ、値にvalueをいれます。データが多い時は事前確率を仮定する必要はありませんが、データがまだ集まっていない場合は、事前情報を入力し事前確率を仮定するのがおすすめです。具体的には過去のCRの平均値、標準偏差を入れます。

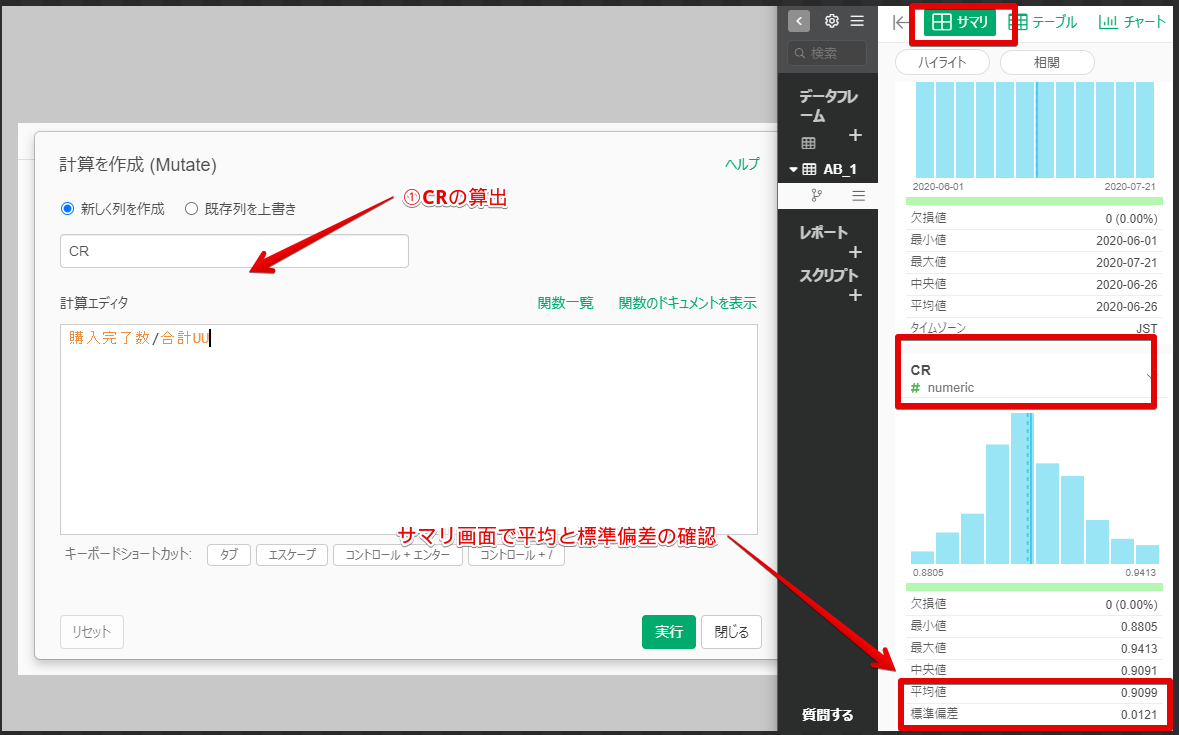
過去のCRの平均値、標準偏差（＝事前情報）の算出方法

①CRの算出=購入完了数/合計UU数（購入開始ユーザー）②サマリ画面でCRの平均値と標準偏差の確認

結果の確認をしてみます。

このサマリで注目すべき点は「改善する確率」です。Bグループ（従来のままクーポン表示をしない）はAグループに比べて93%優れていると解釈します。また、「期待される改善率」には、AがBよりどれだけ優れているかが示されます。この場合数値は負であるため、「Aグループ＝クーポンが表示させると0.2%コンバージョン率が悪化する」と解釈できます。この0.2％の重要性はECサイトの規模によって重みが変わりますね。一日100万を売り上げるECサイト、一日数億を売り上げるECサイトでは0.2%の重みが変わってきます。重要な判断になりそうです…

ExploratoryでできるベイジアンA/Bテストでは、そのほか改善率の分布なども確認できます。気になる方は先ほどリンクを貼ったExploratoryさんのブログを是非ご覧ください～

さいごに

前篇/後編に分けて、A/Bテストについて『A/Bテスト実践ガイド 真のデータドリブンへ至る信用できる実践とは』をベースにまとめさせて頂きました。少し古い例になりますが、リアル店舗のA/Bテストでぐっとマーケットを広げたワークマンの例などもありますが、何かマーケティング実施したら検証してみるというのは本当に大事ですね。truestarでは様々なデータ分析業務を承っています。こちらからぜひご相談ください。