■はじめに

こんにちは。池田です。

最近統計学の基礎を勉強をしているのですが、何かしらで処理（介入）効果の検証を試してみたいと思いましたので、

Alteryxを使って実際にやってみました。

本日は、効果検証のなかでも基礎である処理効果による2群の平均値の差異と、

その差が統計的に有意であるかをAlteryxで検証する方法について書きたいと思います。

■データの確認

①サンプルデータの準備

サンプルデータはこちらを使ってみます。

データに関する説明も上記のリンク先に記載がありますが、下図で示しておきます。

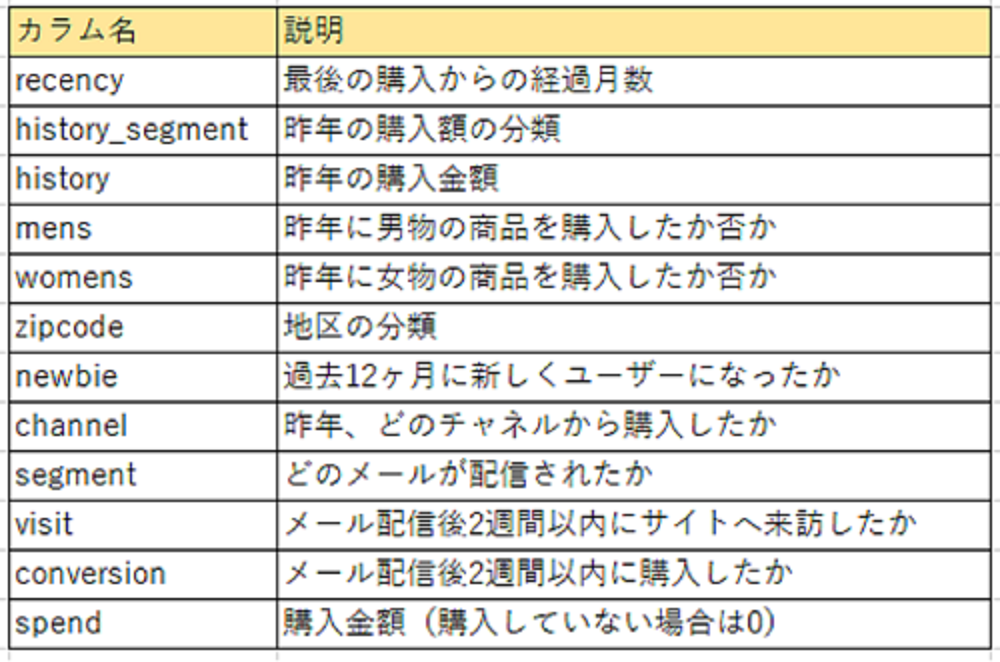
②前提とWFでの処理

今回は男性向けのメールが配信されているものとメールの配信がなかったもので検証しようと思います。

WFで以下の処理を施します。

・女性向けメールが配信されたデータを除きます。

→フィルタツールでSegment列の”Womens E-Mail”データを除きます。

・男性向け配信メールを1、メールの配信がないものを0として介入を表す変数を作成します。

→フォーミュラの条件式を使用してSegment列の”Mens E-Mail”を1、”No E-Mail”を0とします。

（これを”介入”カラムとしておきます）

・介入カラムの各データ（0 or 1）でグループ化を行い、データ数、購入割合、購入金額を算出します。

→集計ツールを使用します。

③結果の確認

WFでの処理結果の確認をします。

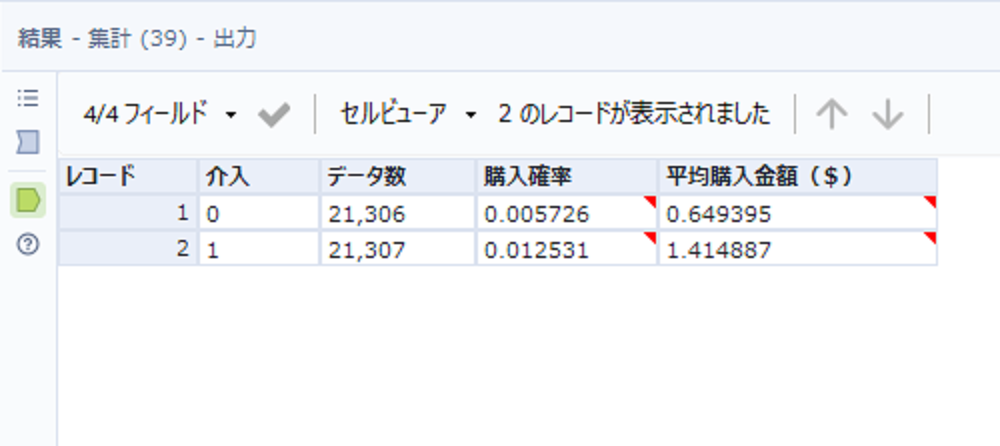
介入があった（介入カラムが1）方が、介入がなかったもの（介入カラムが0）と比較して

購入確率・平均購入金額ともに高いことが確認できます。

つまり、メールが配信されたことで売り上げが発生しやすくなり、その影響のせいか購入金額が上昇していると考えられます。

次のトピックでは、はたしてそれが統計的に有意であるか検証していこうと思います。

■有意差検定Ⅰ（自力で頑張る方法）

①仮説の設定

メールが配信されたグループをA、配信されていないグループをBとし、

各々のグループの購入金額の母平均をμ_A、μ_Bおき、

帰無仮説H₀：μ_A = μ_B　（メールによる購入金額に対する効果がない）

対立仮説H₁：μ_A ≠ μ_B　（メールによる購入金額に対する効果がないとはいえない）

（H₁について、メール配信によって購入金額が上がったとして、μ_A > μ_Bとして片側検定にしてもよいかもしれません）

とします。

②検定統計量の計算

各グループの平均購入金額をx_A、x_Bとします。

2群の平均の差x_A – x_Bは下記で表せます。

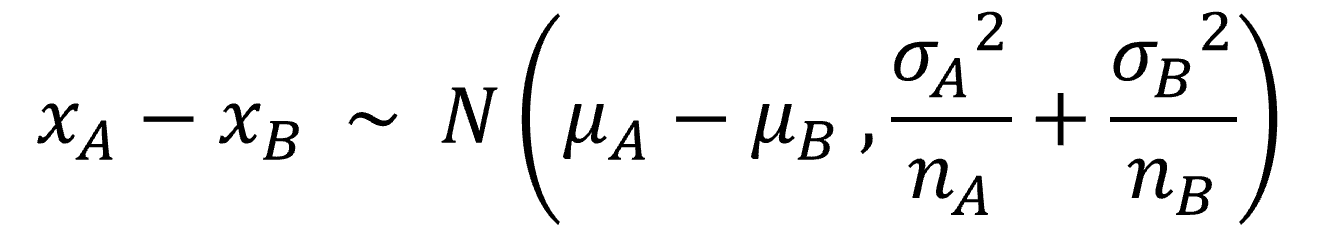
検定統計量をtとすると、下記のように表せて、これは自由度Fのt分布に従います。

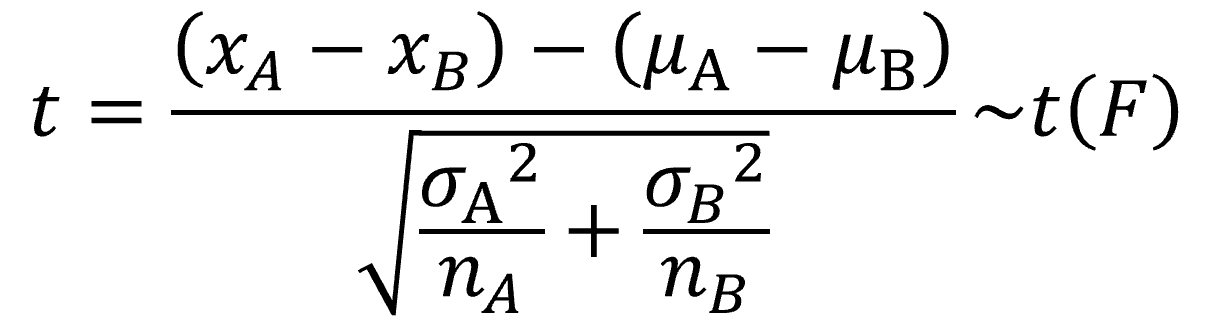
ここで、ｎはサンプルサイズ、σ²は不偏分散を表します。

今回は母分散が未知で、等分散かどうかも不明であるため、ウェルチのt検定を行うことになり、自由度Fは下記の式で求めます。

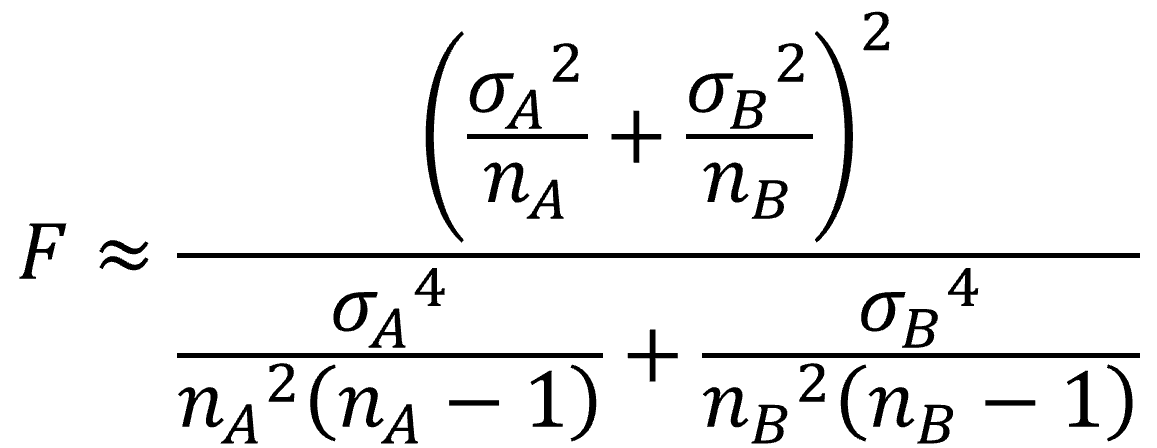
検定統計量tについては、帰無仮説H₀より、μ_A = μ_Bであるので、

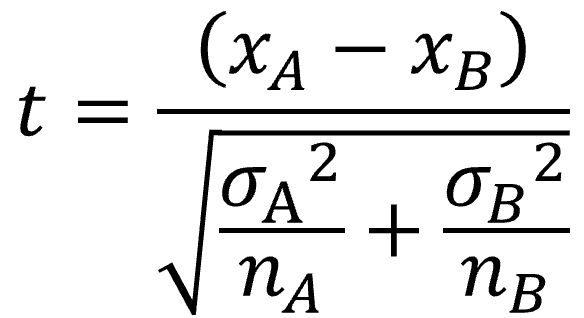
と表せます。これを計算しますと、t ≒ 5.28 となります。

③仮説の判定

自由度Fを先ほどの式から求めると、F ≒ 36666となります。

つまり、自由度36666のt分布で考えて、有意水準5%で両側検定を行うことになりますが、

t分布表では自由度36666のものは見つけられなかったので、代わりに自由度100のt分布表を用いますと、

上側2.5%点は1.9799と求められます。

（※t_0.025(100) > t_0.025（36666）より自由度の小さいものを代わりに使って比較しても大丈夫です）

上記の結果から | 検定統計量t | > t_0.025(100)（> t_0.025(36666)）であるので、検定統計量tは棄却域に含まれます。

よって、帰無仮説H₀は棄却され、各グループの平均購入金額には差があると言えます。

ここまでが通常の解き方になると思いますが、普通にAlteryxでやると結構面倒くさいです（WFは以下のようになりました）。

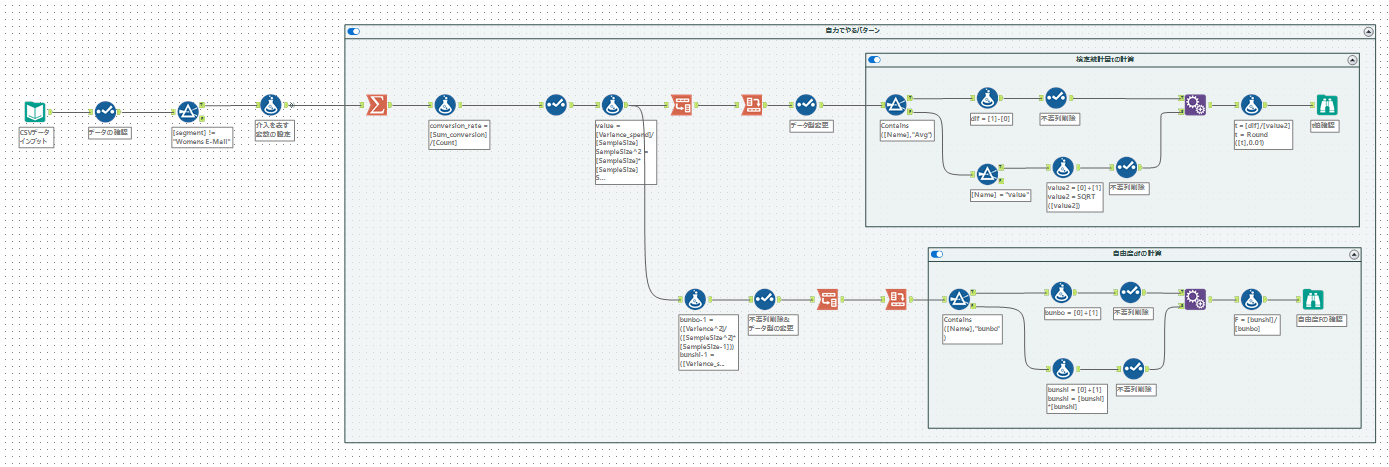
そこで次の有意差検定Ⅱの方法で試してみます。

■有意差検定Ⅱ（t検定ツールを使う方法）

有意差検定ⅠではAlteryxでごりごり計算を行い、自力で検定統計量や自由度を求めましたが、

実はAlteryxでt検定を行いたい場合、「t検定」というたいへん便利なツールがあります。（そのまんまですね）

これは、予測ツール群の中に入っています。

これを使用して、メールを配信したグループ（A）と配信しなかったグループ（B）の平均購入金額に関するt検定を実施します。

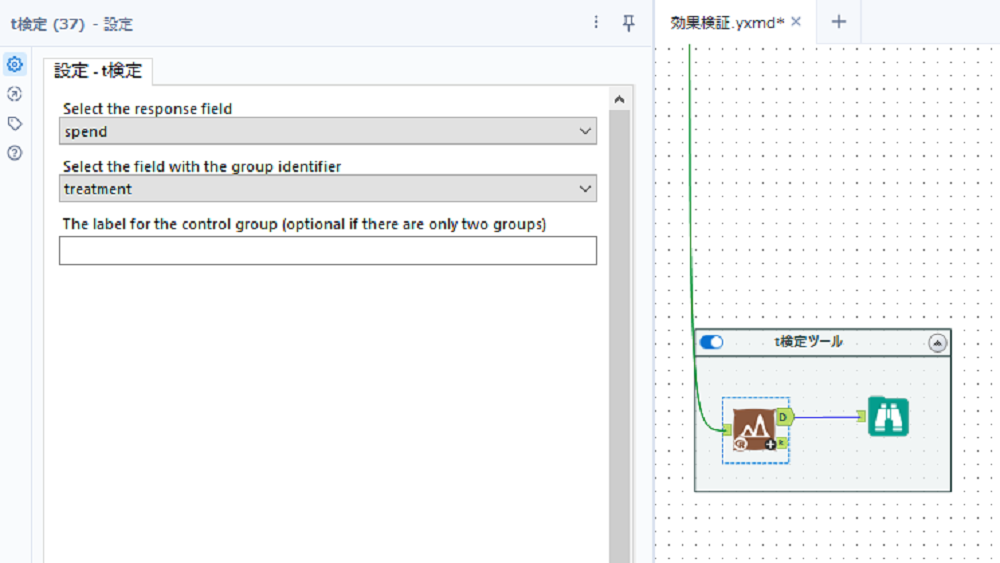
以下はツールの説明です。

・select the response field（日本語：応答フィールドを選択）

→群固有の平均を計算して比較したいカラムを選択します。今回で言うとspendカラムですね。

・Select the field with the group identifier（日本語：グループ識別子の付いたフィールドを選択）

→今回でいう介入カラムのように、グループ化して比較したいカラムを選択します。

・The label for the control group (optional if there are only two groups)（日本語：対照群のラベル (群が 2 つのみの場合はオプション)

→2群の場合は特に指定する必要はありません。（オプション的に比較群を設定したい場合のみ使用します。）

結果は出力側のDアンカーから確認できて、以下のようになります。

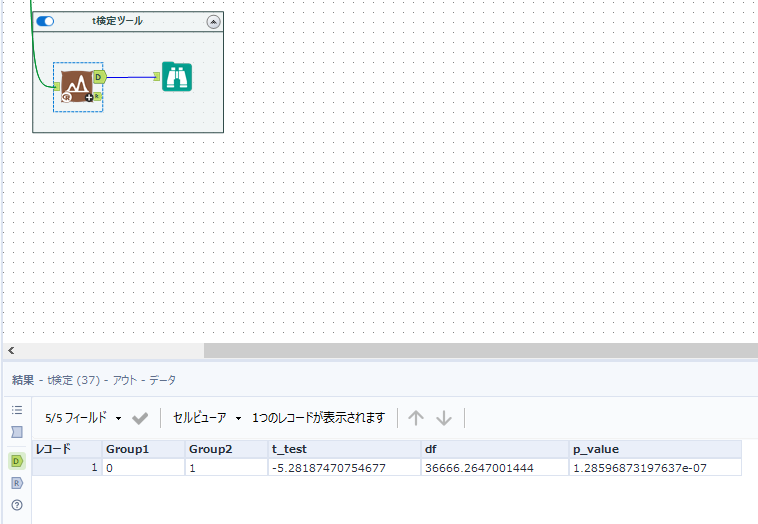
有意差検定Ⅰとは群の設定（A、Bの設定）が逆になっているため、検定統計量tは負の値をとっていますが、

検定統計量tの絶対値、自由度dfともに有意差検定Ⅰで求めたものと同じ値が確認できます。

また、p値が有意水準で定めた5%よりも非常に小さいことから、設定した仮説（帰無仮説）が棄却できることも確認できます。

このようにt検定ツールを使用することで、簡単に（あっさりと）検定統計量、自由度、p値を算出することができます。

※処理全体のWFは以下のようになりました。

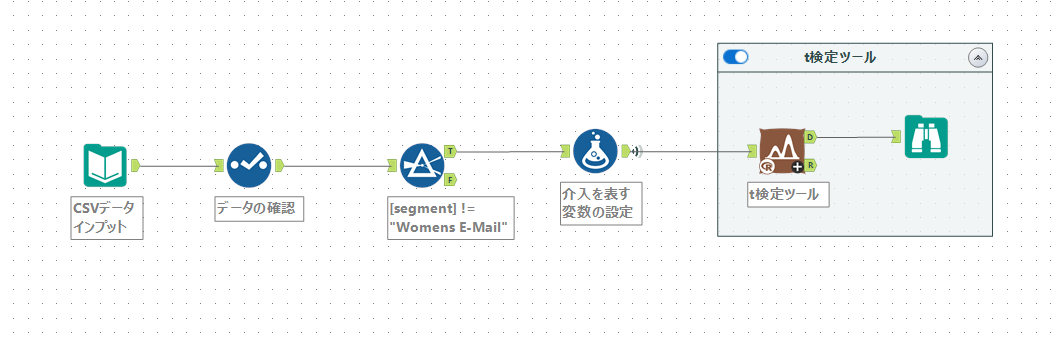
■まとめ

自力で行うとたいへんなt検定でもAlteryxのツールを使えば、簡単に必要な値を求めることができます。

ただやはり、そのツールでやっていることの考え方などの背景は知っておきたいなと思います。

Alteryxの予測ツール群の中には、他にもF検定や回帰分析系などの便利なツールが多いので、

引き続きいろいろ使って試していきたいなと思います。